Sky Coordinates

What are Latitude and Longitude? 

Latitude tells us how far north or south a point on the Earth is. There are 180° degrees of latitude. These range from 90° South at the South Pole to 90° North at the North Pole. The Earth's equator has a latitude of 0°. The equator is an imaginary line around the Earth's centre, dividing it into two equal parts: the Northern and Southern Hemisphere. 

Longitude tells us how far west or east somewhere is. Because the Earth is a sphere, there are 360 degrees of longitude. These range from 180° East to 180° West. The Greenwich Meridian, which runs through the Royal Observatory Greenwich in London, is where the longitude is 0°. It is called the Prime Meridian and is an imaginary line dividing Earth into two equal parts: the Eastern and Western hemispheres. 

Using these coordinates, we can describe a position anywhere in the world. For example, the centre of Liverpool has a latitude of 53.3° North and a longitude of 2.8° West, which we write as 53.3°N, 2.8°W. 

We can use similar systems to find objects in the night sky. We call these celestial coordinates. 

What are celestial coordinates? 

Imagine that the Earth is at the centre of a huge sphere in space. Then, imagine that all the objects we see in the night sky are held at points on the sphere. This imaginary sphere is known as the celestial sphere. We can measure locations on the sphere using two main coordinate systems

(1) The Altitude-Azimuth Coordinate System 

The Altitude-Azimuth system measures objects' vertical (altitude) and horizontal (azimuth) positions in the sky. 

• Azimuth (Az): This tells you an object's horizontal, or side-to-side, position in your 360° field of view. It is measured starting in the north, so an object to the north has an azimuth of 0°. The angle increases the further clockwise an object is from the north. So, for an object to the East, the angle is 90°. For an object to the south, it is 180°. Finally, for an object to the West, it would be 270°. 

• Altitude (Alt): This tells you the vertical (up and down) position: how far the object is above the horizon. So, for an object on the horizon, it would be 0°. Or for an object directly above the observer, 90°. This point directly overhead is called the zenith. 

The Altitude-Azimuth system is sometimes called a horizontal system because the coordinates are relative to the horizon rather than fixed to the stars. This means that any measurements using this system are dependent on two things: 

(A) The time and date: Unlike places on Earth, objects in the night sky move over time. This is because the Earth rotates on its axis and orbits the Sun. So, celestial coordinate systems must take this movement into account. 

The altitude helps see when an object is visible in the night sky, and it can be used to work out when an object rises and sets in the sky. When an object's altitude is 0°, it rises or sets on the horizon. 

(B) Where the observer is: Your view of the sky changes depending on where you are on the globe. 

For example, stars above the north and south poles appear to circle the pole and never set below the horizon. But, their altitude will change depending on where you are on Earth. The north celestial pole is above your head as if you were standing on Earth's North Pole. If you were standing at the equator, it is on the horizon. 

(2) Right Ascension and Declination

The Right Ascension (RA) and Declination (Dec) system is called an Equatorial system because its coordinates are relative to the centre of the Earth. They do not depend on the observer's location or the time of night. 

However, the Earth's orbit does change over long periods. This means that an object's RA and Dec change slightly each year. When using these coordinates, you must refer to the position of an object on a particular date. The current date used is the J2000, which gives positions relative to where they were on 1st January 2000. 

Just as the Earth has poles and equator, so does the celestial sphere. All points on the celestial equator lie in the same plane as the Earth's equator. 

• Declination (Dec): This measures how far an object is above or below the celestial equator. It is an angle measured in degrees, ranging from -90° (south of the celestial equator) to +90° (north). Because a degree on the night sky can cover a large area, we often need to use smaller angles, called arcminutes and arcseconds. Where 1 degree is 60 arcminutes, and 1 arcminute is 60 arcseconds. 

• Right Ascension (RA): This measures the angle around the celestial equator. RA angle is measured in hours instead of degrees, ranging from 0 to 24 hours. One hour of RA equals 15°. The angle is calculated from a point on the sphere called the vernal equinox. The measurement stops at the point on the celestial equator closest to the object. 

Image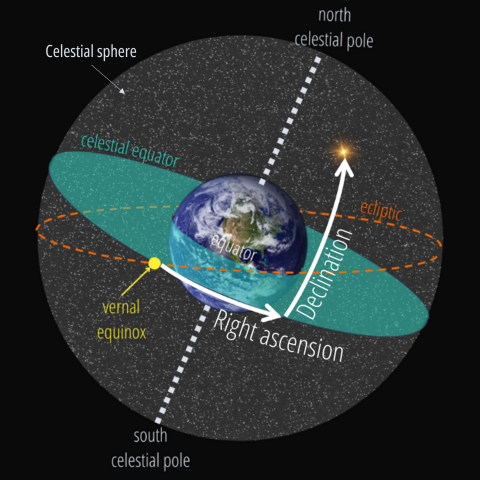

Credit

This work by The Schools' Observatory is licensed under All rights reserved

What is the vernal equinox?

The vernal equinox is a point in the sky where the Sun crosses the celestial equator, an imaginary line above Earth's equator. This crossing happens as the Sun moves from the southern half of the sky to the northern half. It marks the beginning of spring in the Northern Hemisphere. At the vernal equinox, the Sun is at the "first point of Aries," which is used as a starting point to measure the positions of stars and other objects in the sky. 

Here's an example: how do you write the RA and Dec of the bright star Rigel?

RA = 05 14 32 or 05 hours 14 minutes 32 seconds 

Dec = -08 12 06 or -08° 12' (arcminutes) 06" (arcseconds)